
알고리즘
알고리즘 역사 특성 효율성 - 설명하는 포스팅을 입니다. 알고리즘을 공부하고 있다면 알아야할 것들이며 만약 틀리거나 잘못된 부분이 있다면 알려주시면 감사하겠습니다.
역사
알고리즘은 이제 일상생활에서도 꽤 자주 볼 수 있는 단어입니다.
알고리즘이라는 용어는 9세기경 페르시아 수학자인 알콰리즈미(al-Khwarizmi)의 이름으로부터 유래되었습니다. 알콰리즈미는 수학의 다양한 방정식들의 해법에 대한 책을 서기 830년에 집필하였으며, 수학 뿐만 아니라 천문학, 지리학, 지도의 제작 발전에도 크게 기여한 학자입니다.
알고리즘은 문제를 해결하기 위한 단계적인 절차를 의미합니다.
흔히 알고리즘은 요리법과 유사하다고 하며, 단계적인 절차를 따라 하면 요리가 만들어지듯이, 알고리즘도 단계적인 절차를 따라 하면 주어진 문제의 답을 주게 됩니다. 주어진 문제에 대해 여러 종류의 알고리즘이 있을 수 있으니, 항상 보다 효율적인 알고리즘을 고안하는 것이 매우 중요하다고 할 수 있습니다.
알고리즘의 특성
입력 : 외부에서 제공되는 자료가 0개 이상 존재합니다.
출력 : 적어도 1개 이상의 서로 다른 결과를 내어야 합니다.
정확성 : 알고리즘은 주어진 입력에 대해 올바른 해를 주어야 합니다. 알고리즘은 모든 입력에 대해 원칙적으로 올바른 답을 출력해야 합니다. 예를 들어, 정렬 알고리즘이 어떤 입력에 대하여 정렬된 결과를 출력하고, 다른 몇몇 입력에 대해서는정렬되지 않은 결과를 출력한다면, 이는 알고리즘이라고 할 수 없습니다.
수행성 : 알고리즘의 각 단계는 컴퓨터에서 수행이 가능하여야 합니다. 알고리즘에 애매모호한 표현이 있으면 프로그래밍언어로 바꿀 수 없게 되어, 컴퓨터에서 수행 시킬 수 없습니다.
유한성 : 알고리즘은 일정한 시간 내에 종료되어야 합니다. 알고리즘의 수행이 끝나지 않거나, 매우 오래 걸리면 현실적으로 해를 얻을 수 없으므로, 알고리즘으로서의 가치를 잃습니다.
효율성 : 알고리즘은 효율적일수록 그 가치가 높아집니다. 알고리즘은 항상 시간적, 공간적인 효율성을 갖도록 고안되어야합니다. 이러한 효율성은 입력의 크기가 커질수록 그 가치가 높아집니다. 하지만 비효율적인 알고리즘도 알고리즘이므로, 효율적인 알고리즘만이 알고리즘이라고 할 수 없습니다.
가장 오래된 알고리즘
가장 오래되 알고리즘은 기원전 300년경에 만들어진 유클리드(Euclid)의 최대공약수를 찾는 알고리즘입니다. 최대공약수는 2개 이상의 자연수의 공약수들 중에서 가장 큰 수 입니다.
유클리드는 2개의 자연수의 최대공약수는 큰 수에서 작은 수를 뺀 수와 작은 수와의 최대공약수와 같다는 성질을 이용하여 최대공약수를 찾았습니다.
예를 들어 26과 14의 최대 공약수는 26-14=12과 작은 수 14와의 최대공약수와 동일하다. 유클리드는 이 과정을 반복하여 최대공약수를 계산하였습니다. 계속 빼가면서 계산하여 0과 같이 나오는 숫자가 최대공약수가 되는 것입니다. 계속 계산을 해본다면
최대공약수 26, 14
26-14 =12
14-12 =2
12-2 =10
10-2 =8
8-2 =6
6-2 =4
4-2 =2
2-2 =0 최대공약수 2입니다.
최대공약수144, 24
144-24 =120
120-24 =96
96-24 =72
72-24 =48
48-24 =24
24-24 =0 최대공약수 24입니다.
알고리즘의 효율성 표현
알고리즘의 효율성은 알고리즘의 수행 시간 또는 알고리즘이 수행하는 동안 사용되는 메모리 공간의 크기로 나타낼 수 있습니다. 이것은 시간복잡도(time complexity, 공간복잡도(space complexity)라고 합니다.
일반적으로 알고리즘들을 비교할 때에는 시간복잡도가 주로 사용됩니다. 제가 생각하기에 공간복잡도는 같은 메모리를 두면 되기 때문에 얼마나 빠른 시간 안에 수행해낼 수 있는가를 보는 것이 비교가 잘 되기 때문에 시간복잡도를 사용하는 것 같습니다.
알고리즘을 프로그램으로 구현해서 이를 컴퓨터에서 실행시켜 수행된 시간을 측정할 수도 있습니다. 그러나 실제로 측정된 시간은 알고리즘을 수행하는 데 여러 가지 변수가 있으므로, 알고리즘의 효율성을 객관적으로 평가하기 어렵습니다.
왜냐하면 어떤 컴퓨터에서 수행시켰는지, 어떤 프로그래밍 언어를 사용했는지, 얼마나 숙련된 프로그래머가 프로그램을 작성했는지 등에 따라 실제 수행 시간은 달라질 수 밖에 없기 때문입니다.
효율성 표현 및 복잡도
알고리즘의 복잡도를 표현하는 방식에는 최악 경우 분석(worst case analysis), 평균 경우 분석(average case analysis), 최선 경우 분석(best case analysis) 등이 있습니다. 일반적으로 최악 경우 분석으로 알고리즘의 복잡도를 나타냅니다. 최악 경우 분석은 '어떤 입력이 주어지더라도 얼마 이상을 넘지 않는다' 라는 표현입니다. 평균 경우 분석은 입력의 확률 분포를 가정하여 분석하는데, 대부분의 경우 균등분포를 가정합니다. 즉, 입력이 무작위로 주어진다고 가정하는 것입니다. 최선 경우 분석은 경우는 거의 사용되지 않으며, 최적 알고리즘을 고안하는데 참고자료로서 활용되기도 합니다.
복잡도의 점근적 표기
시간(또는 공간)복잡도는 입력 크기에 대한 함수로 표기하는데, 이 함수는 주로 여러 개의 항을 가지는 다항식입니다. 그래서 이를 단순한 함수로 표현하기 위해 점근적 표기를 사용합니다.
점근적 표기란 입력 크기 n이 무한대로 커질 때의 복잡도를 간단히 표현하기 위해 사용하는 표기법입니다. 단순한 함수로 변환하는 예를 들면,


을
으로
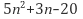
을 으로 2n+3을 n으로 단순화시킵니다. 공통점은 다항식의 최고차항만을 계수 없이 취한 것입니다. 이 단순화된 식에 상한, 하한, 동일한 증가율과 같은 개념을 적용하여 점근적 표기를 사용합니다.
O (Big-Oh)-표기, Ω (Big-Omega)-표기, θ (Theta)-표기
O-표기는 복잡도의 점근적 상한을 나타내고, Ω-표기는 복잡도의 점근적 하한을 나타내며, θ-표기는 복잡도의 상한과 하한이 동시에 적용되는 경우를 나타냅니다.
점근적 상한, 하한, 동시에 대한 것이 이해가 안될 수도 있는데 점근적이라는 말 자체가 n을 무한대로 증가시킨다는 이야기입니다. 이러한 점근적 표기를 사용하여 알고리즘의 효율성을 비교할 수 있습니다. O-표기로만 이야기를 해보겠습니다.

과

의 함수(c는 상수)가 있다고 가정한다면 교차점 이후로는
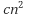
의 값이

보다 크다고 할 수 있습니다.
따라서 O() 이 의 점근적 상한이 되는 것입니다. 이러한 복잡도에 대해서는 그림을 포함하여 나중 포스팅에서 다시 설명을 하도록 하겠습니다. (설명할 것이 많기 때문입니다.) 또한 기본적인 알고리즘을 포함하여 예를 들어 설명하도록 하겠습니다.
▼ 도움이 되셨다면 공감 또는 댓글을 남겨주시면 작성자에게 힘이 됩니다.
▼ 문의사항 댓글도 환영합니다.
'IT' 카테고리의 다른 글
| 어도비 플래시, 2020년에 지원중단 (0) | 2017.07.27 |
|---|---|
| 라즈베리파이 운영체제(OS) 설치 방법 - 라즈비안 (0) | 2017.07.25 |
| Vi 편집기 설명과 조작법, 커서이동 (0) | 2017.07.24 |
| 편리함을 추구한 달러쉐이브클럽 (0) | 2017.07.23 |
| GNU/Linux - 역사 및 특징 (0) | 2017.07.13 |




댓글